Mean Calculator

The mean calculator determines the mean (average), median, mode, range, and many other values of a given set of numbers.

Mean:
Median:
Mode:
Range:
Geometric Mean:
Root Mean Square:
Min. Value:
Max. Value:
Count:
Sum:
Related Median Calculator Average Calculator Standard Normal Table

How to Use the Mean Calculator?

  1. Firstly, input the data set with a space or a comma separator. For example: 11 12 13 14 15 or 11, 12, 13, 14, 15.
  2. The tool supports integer, decimal, fractional, and negative values.
  3. Press the 'Calculate' button and get the mean and other statistical values for the entered data set.
  4. For a new calculation, press the 'Reset' button.

What is Mean?

The mean is the average value of a set of numbers. It's also used to analyze the variability of data. In the context of statistics and probability, the mean represents the "Central Tendency" of a group of elements. Also, it's beneficial for examining the common characteristics between the elements in a collection.

Mean Formula:

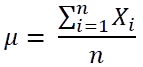
Mean Formula

Where,

μ = mean.

n = total number of elements in the data set.

Count = sum of all the elements (from the first element to the nth element).

How to Calculate Mean?

Let's take an example.

Example:

Calculate the mean for this data set: 7, 3, 1, 7, 4.6, 6.2, 10, 10.4, 7.5, 9.1

Solution:

Step 1: Initialize the value of 'n'

n = number of elements present in the data set.
So, n = 10.

Step 2: Find the sum of data set

Xi = 7 + 3 + 1 + 7 + 4.6 + 6.2 + 10 + 10.4 + 7.5 + 9.1 = 65.8

Step 3: Divide the sum of data set (Xi) by the total number of the elements (n)

μ = Xi / n = 65.8 / 10 = 6.58

So, the mean (μ) = 6.58.

You can use our mean calculator to perform the above calculation with ease.